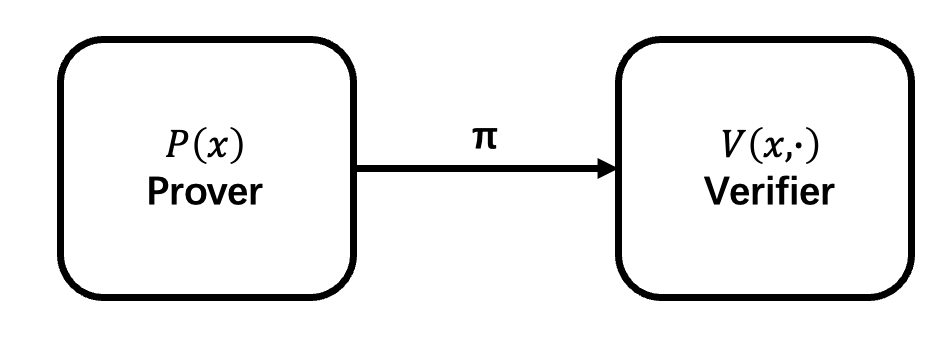
Interactive Proof

在本篇笔记中，笔者参考CS294课程详细记录了交互式证明的定义、性能等并自行补充了一些内容，主要分为以下几个部分，读者可以根据自己需要进行判断

• 交互式证明的定义、GNI的交互式证明协议、\(\mathrm{P}\subseteq \mathrm{PSPACE}\)​
• Sumcheck协议、\(\mathrm{co-NP}\subseteq \mathrm{IP}\)、\(\mathrm{P^{\#P}}\subseteq \mathrm{IP}\)
• QBF的定义、\(\mathrm{PSPACE}\subseteq \mathrm{P}\)、\(\text{TQBF}\in \mathrm{PSPACE-complete}\)​
• Public coin、Arthur-Merlin、\(\mathrm{GNI}\in \mathrm{AM[2]}\)、\(\mathrm{IP[k]}\in \mathrm{AM[k+2]}\)​
• 通信复杂度限制下的IP
• Doubly-efficient Interactive Proof
• 零知识交互式证明

Definition

我们还是首先从我们最熟悉的NP出发，NP指确定型图灵机可以在多项式时间内验证（decidable）的判定问题集合。

形式化定义如下： \[ \begin{align*} L &\in \mathrm{NP} \iff \exists \text{ polynomial-time } \mathrm{decider \,D} \text{ s.t.}\\ \text{(1) } &\forall \text{ instance } x\in L, \, \exists \text{ witness } \omega \quad D(x,\omega)=1\\ \text{(2) } &\forall \text{ instance } x\notin L, \, \forall \text{ witness } \omega \quad D(x,\omega)=0 \end{align*} \] 我们对首先仔细观察一下NP的定义，对于某一个实例（或论述，statement），我们生成一个证据（或赋值，assignment），判定者可以在多项式时间内，根据实例和证据验证实例是否属于语言\(L\)。

这种表述与数学证明十分相似（Mathematical Proof），给定一个定理，我们生成一个证明，验证者可以十分高效的根据我们的证明判定定理是否正确。

我们可以进一步思考定义中隐含的一些信息：

• NP问题只要求给定一个证据，我们能够高效地验证证据的正确性，而不考虑获取证据的难度。因此，我们对于Prover的计算资源是没有限制的，对于Verifier的计算资源，我们要求是多项式时间的
• 由于Verifier是多项式时间的，所以证据的大小也应为多项式大小，否则仅仅是读取就已经超出了Verifier的能力。
• 在这样的证明系统中，Verifier和Prover之间没有交互，Verifier只读取了Prover给出的证据
• Verifier和Prover都没有使用Randomness，然而Randomness是一个非常强大的工具，在实际情况下这个限制貌似没有那么必要。

因此，我们可以对NP进行一些改变，提高NP的能力：

• 允许Verifier和Prover之间进行交互；
• 允许Verifier和Prover使用Randomness。

从而我们就得到了交互式证明（Interactive Proof，IP）

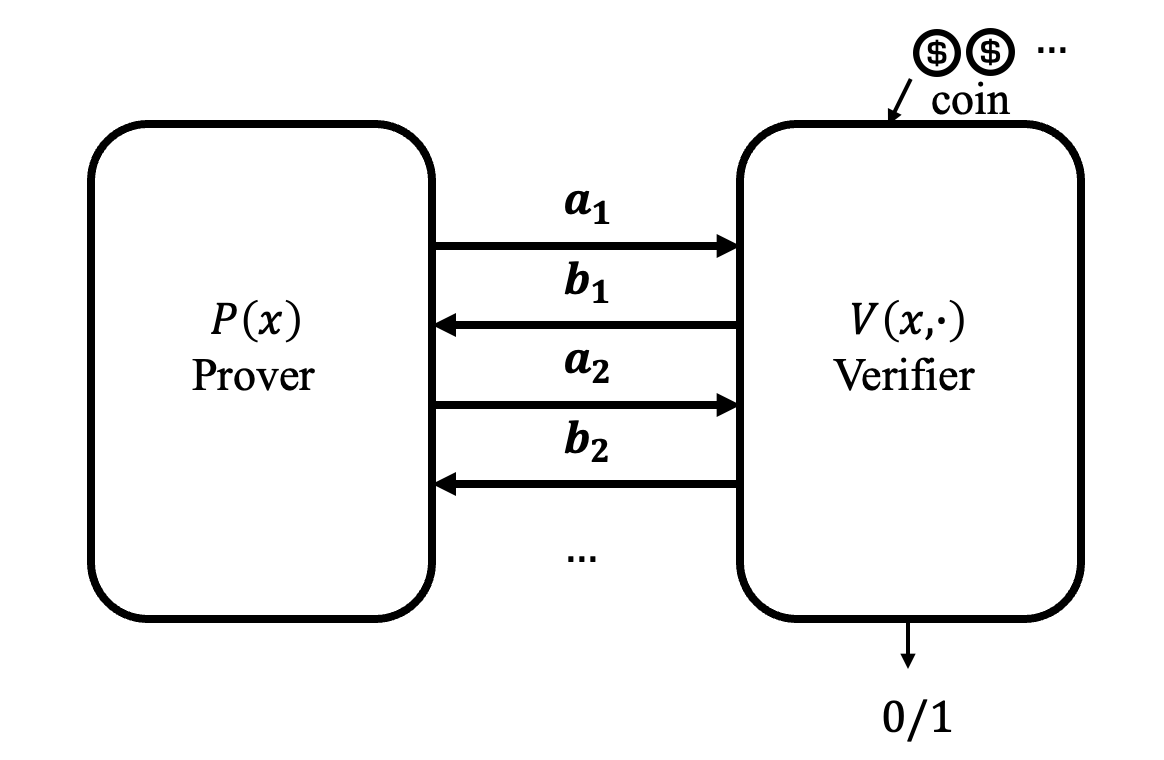
形式化定义如下：

语言\(L\)的IP是一个二元组\((P,V)\) ，满足以下性质：

• 完备性（Completeness）：\(\forall x\in L,\, \text{Pr}_r[<P(x),V(x,r)>=1]=1\)
• 稳健性（Soundness）：\(\forall x\notin L,\, \text{Pr}_r[<\widetilde{P},V(x,r)>=1]\leq1/2\)

其中，\(P\)为unbounded honest Prover，\(V\)为efficient honest Verifier，\(1\)和\(1/2\)可以被其他值代替，允许一定的error存在，只需要完备性和稳健性之间具有明显的差别（gap）即可。

在提出IP的定义之后，我们首先想到的问题就是IP的能力相对于NP怎么样？有什么样的提升？

笔者在看到IP的定义之后想到的是一方面，IP本身就是从NP定义上拓展来的，所以IP肯定能力会比NP强，另一方面，允许一定的error存在和BPP比较类似，所以应该也会包含BPP

我们首先给出来一个非NP问题GNI的交互式证明，来熟悉一下交互式证明到底是什么样的

IP for Graph Non-Isomorphism

我们首先对图同构问题（Graph Isomorphism，GI）给出定义：

假设\(G_0(V,E_0)\)和\(G_1(V,E_1)\)为关于点集\(V\)的两个图（Graph），如果存在一个置换 \[ \pi:V\rightarrow V s.t.\\ (u,v)\in E_0 \leftrightarrow (\pi(u),\pi(v))\in E_1 \] 我们有\(G_0\equiv G_1\)（\(G_0\)和\(G_1\)同构），写作\(G_0=\pi(G_1)\)

我们定义：图同构问题\(\mathrm{GI}:=\{(G_0,G_1)\mid G_0\equiv G_1\}\)，图非同构问题（Graph Non-Isomorphism，GNI）\(\mathrm{GNI}:=\{(G_0,G_1)\mid G_0\not\equiv G_1\}\)

对于GI和GNI问题，我们有以下结论：

• \(\mathrm{GI}\in \mathrm{NP}\)
• \(\mathrm{GNI}\in\mathrm{coNP}\)

接下来，我们通过给出GNI问题的交互式证明来说明\(\mathrm{GNI}\in\mathrm{IP}\)：

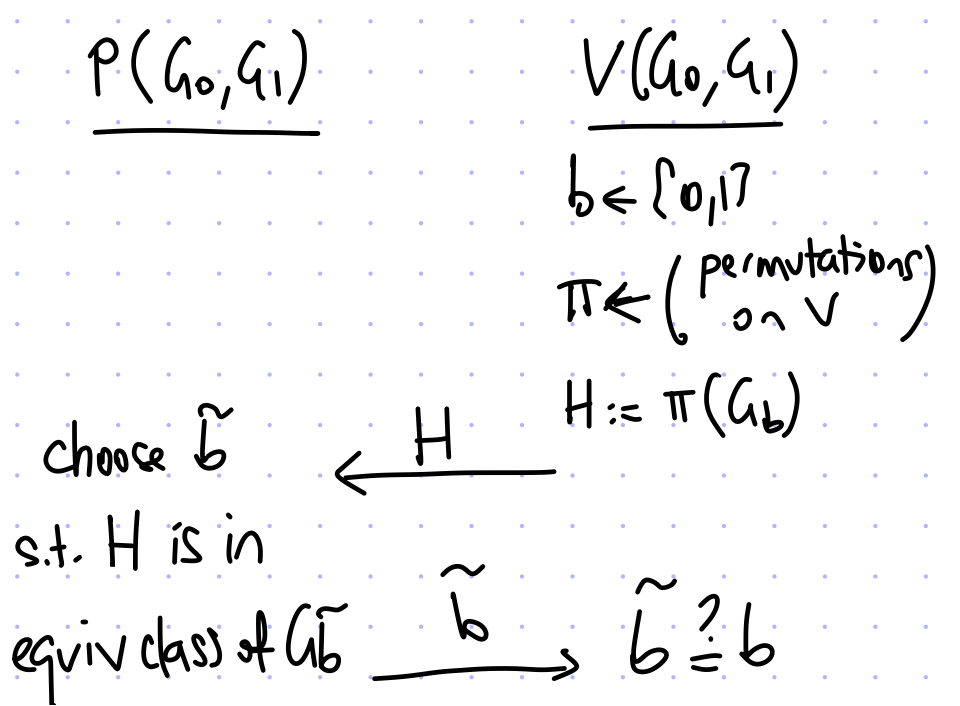
[!NOTE]

• 我们忽略Prover生成\(\widetilde{b}\)的时间
• \(b\)的机密性对于该协议至关重要

我们对于协议的完备性和稳健性进行分析：

​ Completeness：\((G_0,G_1)\in \mathrm{GNI},\, [G_0\not\equiv G_1]\)，\(G_0,G_1\)位于不同的同构等价类，因此Prover可以轻松地区分\(H\)与\(G_0,G_1\)中的哪一个同构，从而给出正确的\(\widetilde{b}=b\)，\(Pr[\widetilde{b}=b]=1\)

​ Soundness：\((G_0,G_1)\notin \mathrm{GNI},\, [G_0\equiv G_1]\)，\(G_0,G_1\)位于同一个同构等价类，因此对于任何Prover都无法区分\(H\)由\(G_0,G_1\)中的哪一个推出，在Prover看来两者是相同的，只能给出一个随机的的\(\widetilde{b}\)，\(Pr[\widetilde{b}=b]=1/2\)

综上，我们给出了一个coNP问题GNI的交互式证明，在此过程中，我们也熟悉了交互式证明到底是什么样的，接下来我们将给出IP的上界

An Upper Bound on IP

我们首先给出结论：\(\mathrm{IP}\subseteq \mathrm{PSPACE}\)

PSPACE是计算复杂度理论中能被确定型图灵机利用多项式空间解决的判定问题集合，包含所有能用多项式大小内存解决的问题，在PSAPCE类的问题中，你不在乎时间，只关心算法所需的内存空间。

接下来我们给出证明，这个证明十分有趣：

证明：

令\({L}\in \mathrm{IP}\)，且\((P,V)\)是一个关于\(L\)的\(\mathrm{IP}\)，我们现在需要证明\(L\in \mathrm{PSPACE}\)，我们假设具有一个实例\(x\)，并且定义\(q_x :=\max\limits_{\widetilde{\text{P}}}\text{Pr}_r[<\widetilde{\text{P}},V(x)>=1]\)，我们有

1. 如果\(x\in L\)，有\(q_x=1\)
2. 如果\(x\notin L\)，有\(q_x\leq 1/2\)

现在我们可以将原有的证明\(L\in \mathrm{PSPACE}\)的问题规约为证明\(q_x\)可以在多项式空间内运算的问题，但是仍然存在一个问题：我们不能遍历所有的Prover，因为有一些Prover并不是\(\mathrm{PSPACE}\)的。

我们考虑到由于所有的Verifier一定是\(\mathrm{P}\)的，因此所有Prover与Verifier交互的transcript一定是polynomial size的（Verifier需要在polynomial time的情况下读取它），因此我们可以不考虑遍历所有的Prover，而是遍历所有的transcript。由此最优Prover就可以在\(\mathrm{PSPACE}\)下进行运算，从而\(q_x\)也可以。

我们假设transcript可以写作元组（tuple）的形式\((a_1,b_1,a_2,b_2,\dots,a_i,b_i)\)

我们定义算法\(P^*(x,(a_1,b_1,\dots,a_i,b_i))\)输出使得Verifier 接受概率最大的下一条消息\(a_{i+1}\)，我们首先假设\(P^*\in \mathrm{PSPACE}\)，由此我们可以证明\(q_x \in \mathrm{PSPACE}\)​，证明如下：

由于\(P^*\)是使Verifier接受概率最大的算法，因此我们可以得到\(q_x=\dfrac{\sum_{r\in R}d(x,r)}{|R|}\)，其中\(d(x,r)\)为Verifier在输入为\((x,r)\)时，与使用\(P^*\)的Prover交互的结果。

因为Prover为多项式空间，Verifier为多项式时间，因此对于任意一个指定的\(r\)，我们可以在\(\mathrm{PSPACE}\)内计算\(d(x,r)\)

综上所述，如果可以得到如果\(P^*\in \mathrm{PSPACE}\)，我们就得到了\(q_x \in \mathrm{PSPACE}\)，也就是\(\mathrm{P}\in \mathrm{PSPACE}\)

接下来，我们来证明\(P^*\in \mathrm{PSPACE}\)

我们定义\(tr = (a_1,b_1,\dots,a_i,b_i)\)为第\(i\)轮的transcript，\(R[x,tr]\)是和\((x,tr)\)保持一致的随机数\(r\)的集合

\(R(x,tr)\)的意思是，在Verifier已知\((x,tr)\)的情况下，所能选取的随机数的集合，已知知识越多，可选取的随机性越小

我们通过数学归纳法证明：

• \(i=k-1\)

  \(P^*(x,tr)=\mathop{\arg\max}\limits_{a_k} \mathop{E}\limits_{r\in R[x,tr]}[V(x,r,a_1,\dots,a_{k-1},a_k)]\)

  我们可以在\(\mathrm{PSPACE}\)情况下，两层循环遍历所有的消息\(a_k\)和随机数\(r\)。

• \(i<k-1\)（假设当\(|tr|>i\)时，\(P^*\in \mathrm{PSPACE}\)）

  \(P^*(x,tr)=\mathop{\arg\max}\limits_{a_{i+1}} \mathop{E}\limits_{r\in R[x,tr]}[V(x,r,a_1,\dots,a:a_{i+1},a_{i+2}^*,\dots,a_k^*)]\)

  因为当\(|tr|>i\)时，\(P^*\in \mathrm{PSPACE}\)，给定\(a_{i+1}\)，我们可以在多项式空间内计算出\(a_{i+2}^*,b_{i+2}^*,\dots,a_{k}^*\)，之后我们可以遍历\(a_{i+1}^*\)，在多项式空间内计算出最优的\(a_{i+1}^*\)。（\(\mathrm{PSPACE}\)真是太美妙了！）

由此我们可以推导出任意情况下的\(P^*\in \mathrm{PSPACE}\)。

综上，我们就得到了\(\mathrm{IP}\subseteq \mathrm{PSPACE}\)​，证毕

一些小思考

笔者后来又思考了一下，总觉得计算\(q_x\)并不完全等价于\(\mathrm{IP}\)，\(\mathrm{IP}\)的最终目的也不是计算\(q_x\)，笔者的理解是如果\(\mathrm{IP}\subseteq\mathrm{PSPACE}\)，那么\(\mathrm{IP}\)能做到的一些事情，在\(\mathrm{PSPACE}\)的条件下，应该也能做到。就类似于\(\mathrm{NP}\subseteq\mathrm{PSPACE}\)，多项式空间图灵机一定是能做到多项式时间图灵机所能做到的事情的（空间取为\(\log |x|\)即可，\(x\)为多项式时间图灵机的输入），对于NP来说证明是十分简单的，因为NP问题从定义上来看可以只涉及到多项式时间（多项式时间内可验证，只考虑Verifier即可），然而\(\mathrm{IP}\)涉及到交互的问题，要考虑Prover的回复，Prover是具备无限计算资源的，所以我们就要考虑如何在\(\mathrm{PSPACE}\)条件下模拟Prover的行为，通过transcript即可，对于\(\mathrm{IP}\)中的Verifier本身就是高效的，因此我们不需要担心。

Sumcheck Protocol

Sumcheck协议可谓是交互式证明和零知识证明的基石，在本文中，笔者将无比详尽的介绍Sumcheck协议，帮助理解。

我们首先要理解Sumcheck的由来：

从前面一部分中，我们已经了解到了GNI的交互式证明方法，但是GNI并非一个coNP-complete问题。（如果GNI是coNP-complete问题，PH会collapse到2nd level）

在这一节中，我们将进一步拓展，证明$ $和 \(\mathrm{P^{\#P}}\subseteq \mathrm{IP}\)​

\(\mathrm{P^{\#P}}=\) languages decidable in polynomial time via a machine with a \(\mathrm{\#SAT}\) oracle

要证明一个复杂度类属于另一个复杂度类，我们只需要证明前者的完全问题属于后者即可，因此我们需要证明\(\mathrm{UNSAT}\in \mathrm{IP}\)和\(\mathrm{\#SAT}\in \mathrm{IP}\)。

然后这两种问题并不具备GNI问题所具备的等价类性质，无法使用之前的方法进行解决，这是我们就想用一种更通用的方法，能够证明一系列类似的问题。

我们现在唯一能够知道的就是电路对我们来说很复杂，但是我们对多项式是十分熟悉的，我们首先尝试将问题进行算术化，转化为多项式的形式。

Arithmetization of a Boolean Formula

布尔公式\(\phi(x_1,\dots,x_n)\)可以被视作一个树：

• 每一个叶节点都是一个变量\(x_i\)
• 每一个非终端节点都是其子节点的一个运算符（\(\land,\vee,\neg\)）

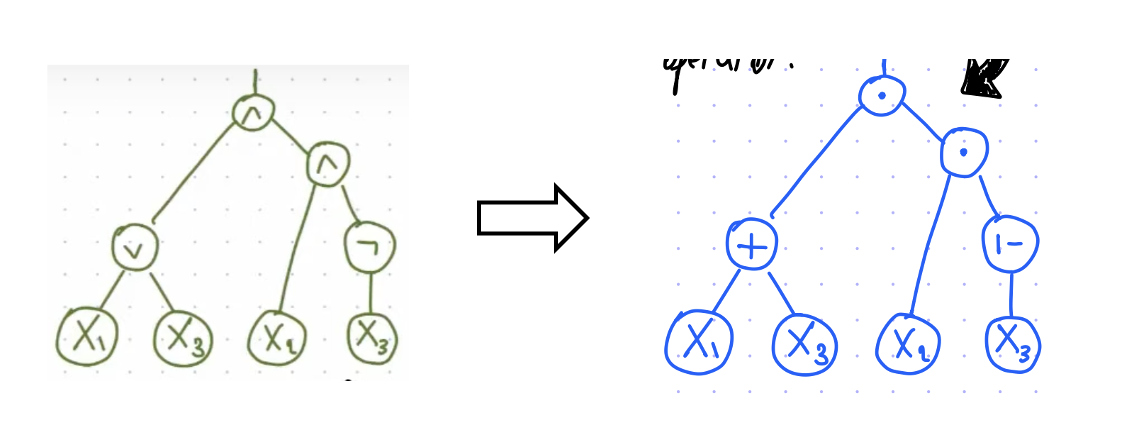
布尔公式（电路）的算术化非常简单，总的来说就是把三种逻辑运算符用算术运算符替换：

• \(\neg x \mapsto {1-x}\)
• \(x\land y \mapsto x\cdot y\)
• \(x \vee y \mapsto x+y\)

因此，我们可以将一个布尔公式\(\phi(x_1,\dots,x_n)\)转化为一个多项式\(p(x_1,\dots,x_n)\)，且该多项式的度\(\deg_{tot}(p)\leq |\phi|\)，我们可以声明一下两个性质：

• \(\phi \in \mathrm{UNSAT} \Rightarrow \sum_{a_1,\dots,a_n\in \{0,1\}}p(a_1,\dots,a_n)=0\)
• \(\phi \not\in \mathrm{UNSAT} \Rightarrow 0 \leq \sum_{a_1,\dots,a_n\in \{0,1\}}p(a_1,\dots,a_n) \leq 2^n3^m\)（以3CNF表示，\(n\)为变量数，m为三元合取范式的数目）

我们有以下推论： \[ \forall \,\text{prime} \, q>2^n3^m,\phi \in \mathrm{UNSAT} \\ \Updownarrow\\ \sum_{a_1,\dots,a_n\in \{0,1\}}p(a_1,\dots,a_n)=0 \mod q \]

Sumcheck Protocol

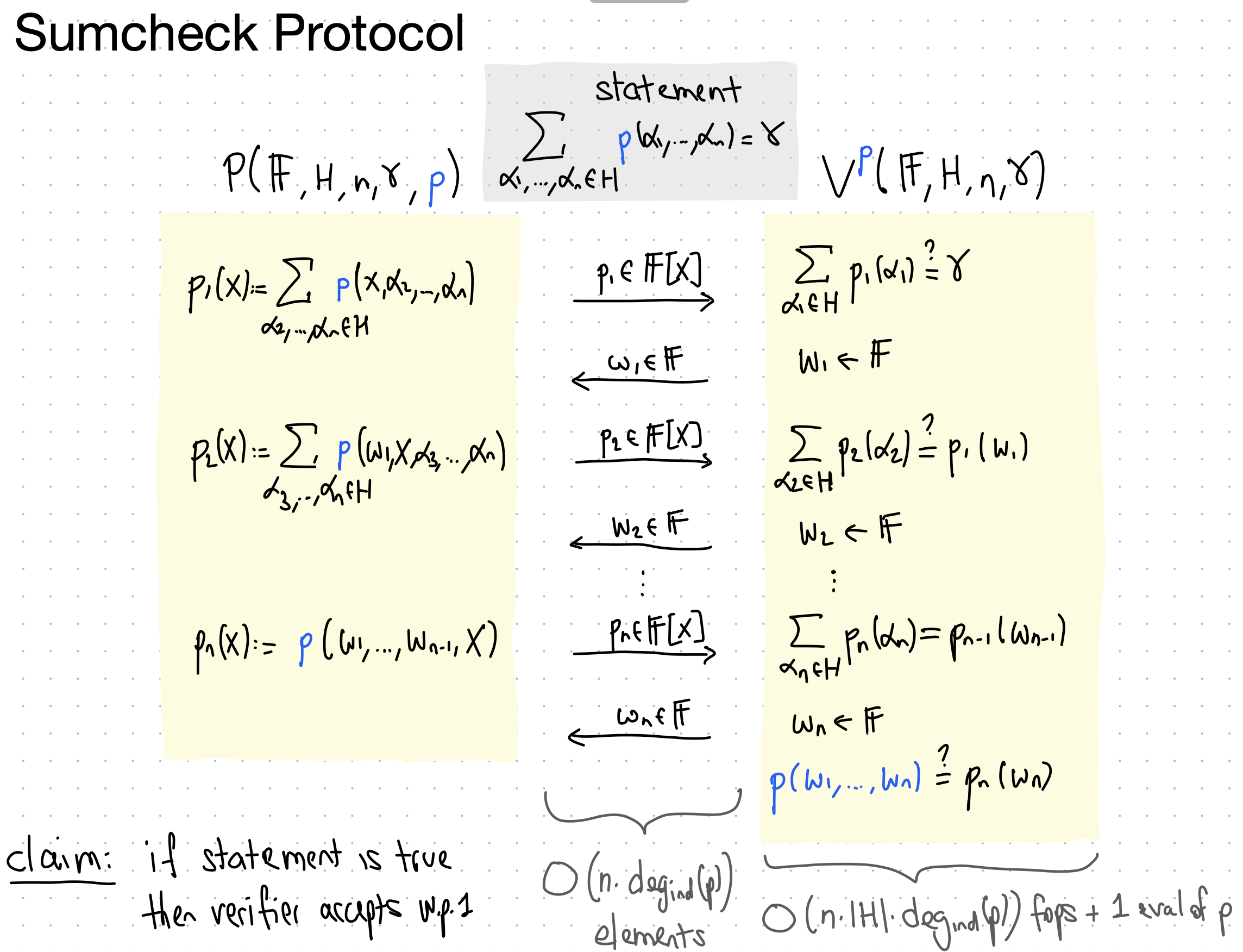
该协议以\(\ell\)回合进行。

• 在第1轮中，\(\mathcal{P}\)发送一个单变量多项式

\[ F_1\left(x_1\right) \stackrel{\text { def }}{=} \sum_{b_2, \ldots, b_{\ell} \in\{0,1\}} f\left(x_1, b_2, \ldots, b_{\ell}\right), \]

\(\mathcal{V}\)检查\(H=f_1(0)+f_1(1)\)。然后\(\mathcal{V}\)将随机挑战\(r_1 \in \mathbb{F}\)发送到\(\mathcal{P}\)。

• 在第\(i\)轮中，其中\(2 \leq i \leq \ell-1，\mathcal{P}\)发送一个单变量多项式

\[ F_i\left(x_i\right) \stackrel{\text { def }}{=} \sum_{b_{i+1}, \ldots, b_{\ell} \in\{0,1\}} f\left(r_1, \ldots, r_{i-1}, x_i, b_{i+1}, \ldots, b_{\ell}\right) \text {, } \]

\(\mathcal{V}\)检查\(f_{i-1}\left(r_{i-1}\right)=f_i(0)+f_i(1)\)，并发送随机挑战\(r_i \in \mathbb{F}\)到\(\mathcal{P}\)。

• 在第\(\ell\)轮中，\(\mathcal{P}\)发送一个单变量多项式

\[ F_{\ell}\left(x_{\ell}\right) \stackrel{\text { def }}{=} f\left(r_1, r_2, \ldots, r_{l-1}, x_{\ell}\right), \]

\(\mathcal{V}\)检查\(f_{\ell-1}\left(r_{\ell-1}\right)=f_{\ell}(0)+f_{\ell}(1)\)。验证器生成随机挑战\(r_{\ell} \in \mathbb{F}\)。给定Oracle，访问\(f\left(r_1, r_2, \ldots, r_{\ell}\right)\)，\(\mathcal{V}\)将接受当且仅当\(f_{\ell}\left(r_{\ell}\right)=f\left(r_1, r_2, \ldots, r_{\ell}\right)\)。Oracle访问的实例化取决于Sumcheck协议的应用。

Completeness

Completeness的证明相对比较简单，如果\(\sum_{\alpha_1,\dots,\alpha_n\in H}p(\alpha_1,\dots,\alpha_n)=\gamma\)，那么一定能够通过Verifier的每一次验证，即以概率为1接受。 \[ \text{if} \,\sum_{\alpha_1,\dots,\alpha_n\in H}p(\alpha_1,\dots,\alpha_n)=\gamma,\text{then }\Pr[\text{Verifier accept}]=1 \]

Soundness

Soundness的证明相对来说就比较复杂，不过有一个直观的想法：如果恶意Prover能够骗过Verifier，那么一定是在存在某一个单变量多项式不同的情况下，使得等式成立了，也就是SZDL，我们单独对于每一个变量使用一次SZDL即可。

Schwartz–Zippel引理：

对于域 \(\mathbb{F}\) 上的每一个阶最多为 \(d\) 的 \(n\) 变元非零多项式, 对于任意有限集合 \(S \subseteq F\) ， \[ \operatorname{Pr}_{r_1, \ldots, r_n \leftarrow S}\left[f\left(r_1, \ldots, r_n\right)=0\right] \leq \frac{d}{|S|} \]

笔者最开始十分不理解为什么是每一个多项式的SZDL之和，而不是之积，毕竟每一次都要骗过Verifier才行，后来才想明白，是因为并不一定是每一个多项式都不相等，所以我们只需要单独考虑每一个多项式不相等的情况，然后逐渐往后推进，即\(p_1\not=p_1^*\)，\(p_2\not=p_2^*|p_1=p_1^*\)就可以覆盖所有\(p\not=p^*\)，但能够欺骗Verifier的情况

接下来我们给出严谨的数学证明： \[ \text{if} \,\sum_{\alpha_1,\dots,\alpha_n\in H}p(\alpha_1,\dots,\alpha_n)\not=\gamma,\text{then }\Pr[\text{Verifier accept}]\leq \frac{n\cdot \deg_{\text{ind}}(p)}{|\mathbb{F}|} \]

Proof：假设有一个恶意的Prover，拥有n个多项式\(\widetilde{p}_1,\dots,\widetilde{p}_n\in \mathbb{F}(x)\)，并且每一个多项式\(\widetilde{p}_i\)取决于之前Verifier的消息\(w_1,\dots,w_{i-1}\in \mathbb{F}\)

我们定义：\(\forall i\in[n], E_i:=\text{"event that } \widetilde{p}_i=p_i\text{"},W=\text{"event that Verifier accepts"}\)

提出以下引理：\(\text{For } j=n,n-1,\dots,1 \,\, \Pr[W]\leq \dfrac{(n-j+1)\cdot\deg_{\text{ind}}(p)}{|\mathbb{F}|}+\Pr[W|E_j \land \dots\land E_n]\)

如果上述引理成立，我们可以轻易地证明我们的结论：我们令\(j=1\) \[ \begin{align} \Pr[W]&\leq \frac{n\cdot\deg_{\text{ind}}(p)}{|\mathbb{F}|}+\underbrace{\Pr[W|E_1 \land \dots\land E_n]}_{ \leq\Pr[W|E_1]=0\, \text{because } \sum_{\alpha_1\in H}\widetilde{p}_1(\alpha_1)=\sum_{\alpha_1\in H} p_1(\alpha_1) \neq \gamma }\\ &=\frac{n\cdot\deg_{\text{ind}}(p)}{|\mathbb{F}|}+0\\ &=\frac{n\cdot\deg_{\text{ind}}(p)}{|\mathbb{F}|} \end{align} \] 接下来我们通过数学归纳法来证明这个引理：

当\(j=n\)时： \[ \begin{align} \Pr[W]&\leq \Pr[W|\overline{E_n}]+\Pr[W|{E}_n]\\ &= \Pr[\text{V accepts }| \widetilde{p}_n \not\equiv p_n]+\Pr[W|{E}_n]\\ &\leq \Pr[\widetilde{p}_n(w_n)=p(w_1,\dots,w_n)| \widetilde{p}_n \not\equiv p_n]+\Pr[W|{E}_n]\\ &= \Pr[\widetilde{p}_n(w_n)=p_n(w_n)| \widetilde{p}_n \not\equiv p_n]+\Pr[W|{E}_n]\\ &\leq \frac{\deg_{\text{ind}}(p)}{|\mathbb{F}|} +\Pr[W|{E}_n] \end{align} \] 假设引理在\(j\in \{2,3,\dots,n\}\)时成立，我们在\(j-1\)时也成立： \[ \begin{align} \Pr[W]&\leq \frac{(n-j+1)\cdot\deg_{\text{ind}}(p)}{|\mathbb{F}|}+\Pr[W|E_j \land \dots\land E_n]\\ &\leq \frac{(n-j+1)\cdot\deg_{\text{ind}}(p)}{|\mathbb{F}|}+\Pr[W|E_{j-1}\land E_j \land \dots\land E_n]+\Pr[W|\overline{E_{j-1}}\land E_j \land \dots\land E_n]\\ &\leq \frac{(n-j+1)\cdot\deg_{\text{ind}}(p)}{|\mathbb{F}|}+\Pr[W|E_{j-1}\land E_j \land \dots\land E_n]+\Pr[\widetilde{p}_{j-1}(w_{j-1})=p_{j-1}(w_{j-1})| \widetilde{p}_{j-1} \not\equiv p_{j-1}]\\ &\leq \frac{(n-j+1)\cdot\deg_{\text{ind}}(p)}{|\mathbb{F}|}+\Pr[W|E_{j-1}\land E_j \land \dots\land E_n]+\frac{\deg_{\text{ind}}(p)}{|\mathbb{F}|}\\ &\leq \frac{[n-(j-1)+1]\cdot\deg_{\text{ind}}(p)}{|\mathbb{F}|}+\Pr[W|E_{j-1}\land E_j \land \dots\land E_n] \end{align} \] 证毕

Interactive Proof of \(\mathrm{UNSAT}\)​

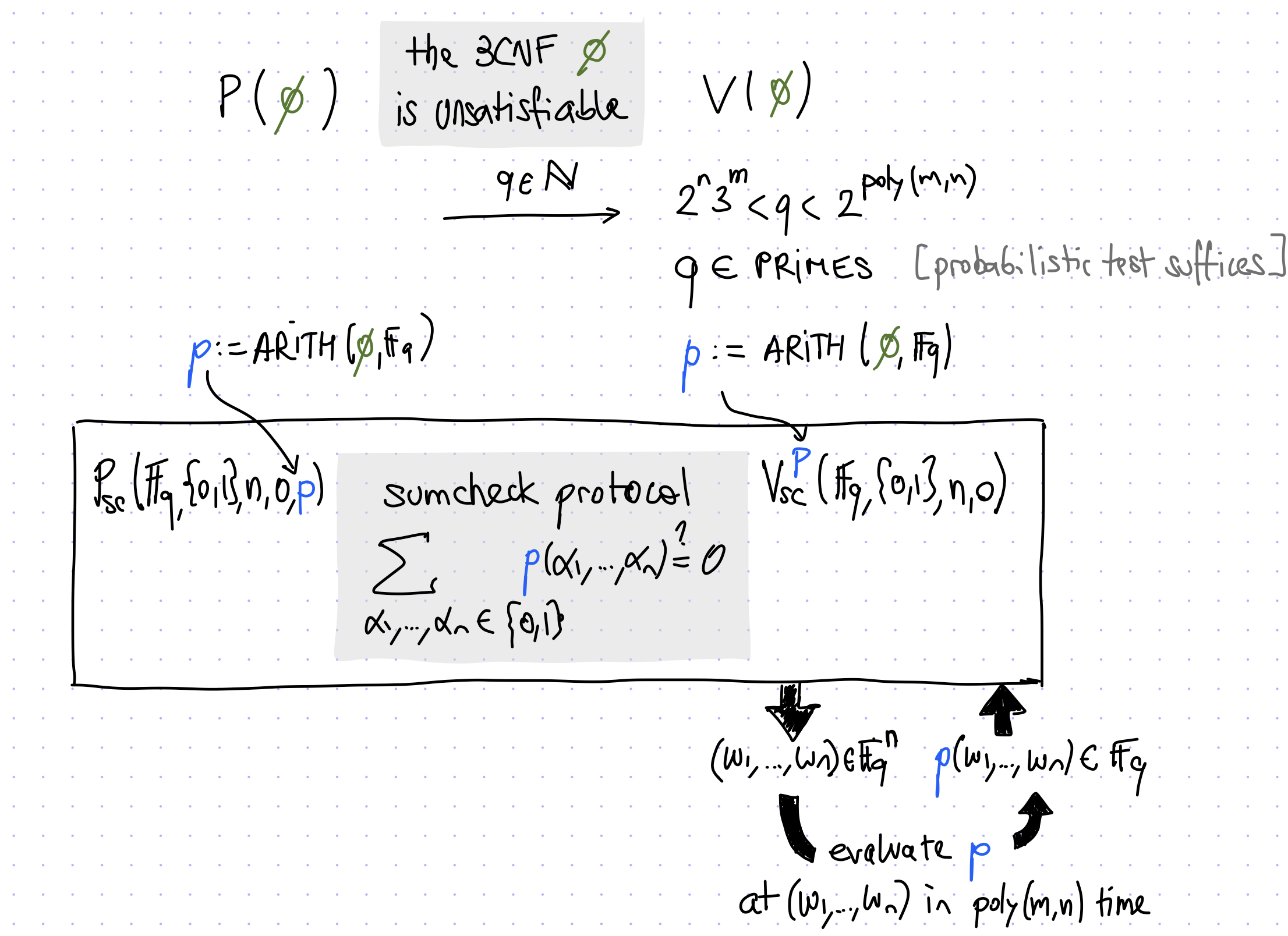
上述协议证明了$ $

Arithmetization for \(\mathrm{\#SAT}\)

在上文中我们提出算术化的方法无法适用于\(\mathrm{\#SAT}\)问题： \[ \forall (a_1,\dots,a_n)\in \{0,1\}^n,\phi(a_1,\dots,a_n)=\text{true}\rightarrow 0<p(a_1,\dots,a_n)\leq 3^m \] 这样会导致我们无法判断满足\(\mathrm{SAT}\)的具体的赋值的数量，因此我们对算术化方法进行以下更改：

• \(\neg x \mapsto {1-x}\)
• \(x\land y \mapsto x\cdot y\)
• \(x \vee y \mapsto x+y-x\cdot y\)

该方法也可适用于\(\mathrm{UNSAT}\)问题，但是有一个微不足道的缺点就是会引入\(xy\)，增加多项式的次数

使用新的算术化方法，我们有： \[ \forall (a_1,\dots,a_n)\in \{0,1\}^n,\phi(a_1,\dots,a_n)=\text{true}\rightarrow p(a_1,\dots,a_n)=1 \] 接下来，我们可以将\(\mathrm{\#SAT}\)规约为以下Sumcheck问题： \[ \forall \text{prime } q>2^n,\#\phi=c \Longleftrightarrow \sum_{(a_1,\dots,a_n)\in \{0,1\}^n}p(a_1,\dots,a_n)=c \mod q \]

Interactive Proof for \(\mathrm{\#SAT}\)

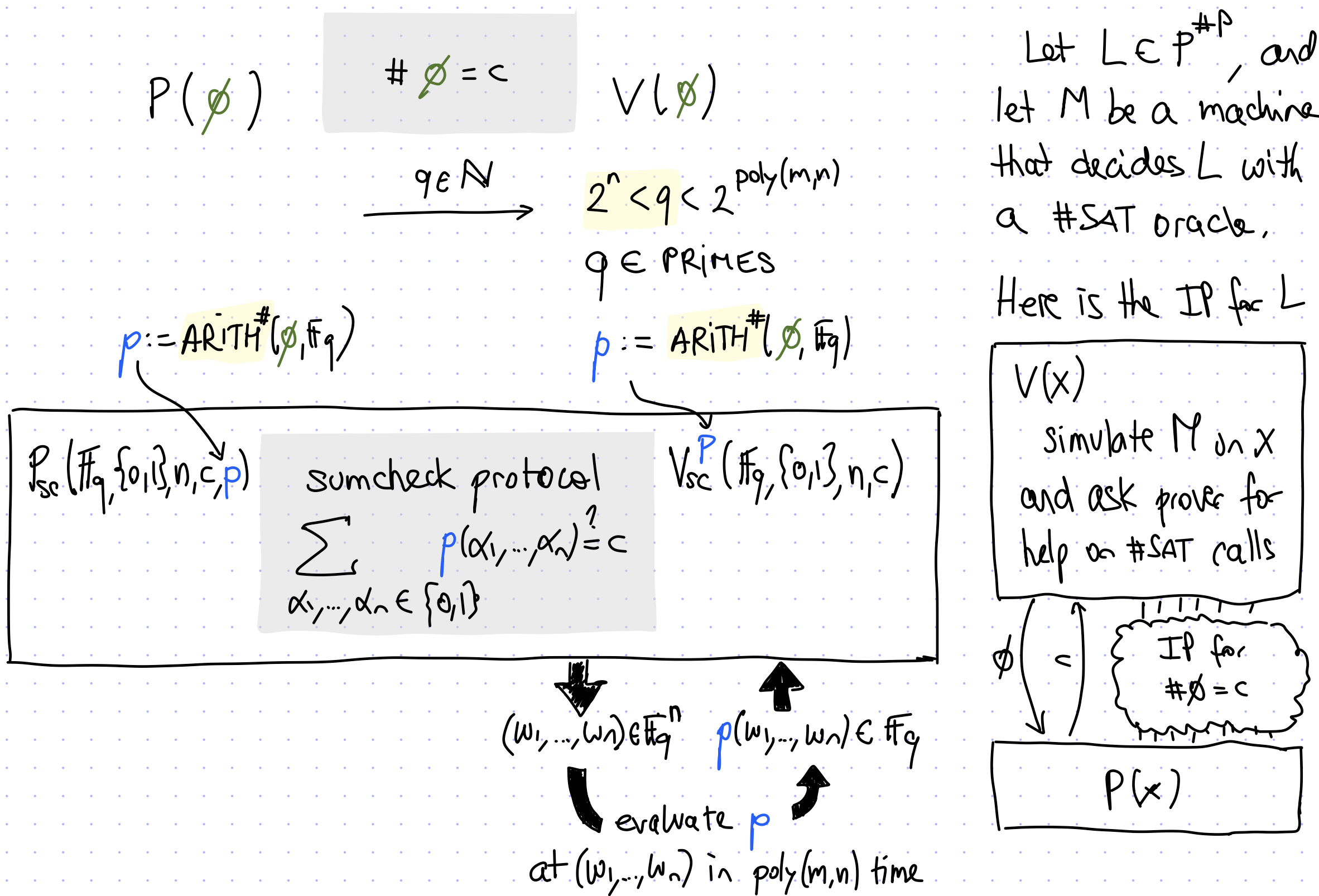
上述协议证明了$ $

现在基础已经十分完备了，接下来我们尝试证明\(\mathrm{IP}\)的下界。

IP=PSPACE

与之前的方法一样，我们还是首先找到一个完全问题，之后将其算术化，最后找到一个IP协议将其解决的方式来证明\(\mathrm{PSPACE}\subseteq \mathrm{IP}\)

步骤	last lecture	today
选择“完全”（complete）问题	\(\mathrm{UNSAT/\#SAT}\)	\(\mathrm{TQBF}\)
算术化	归约为sumcheck问题	归约为sum-product问题
算术问题的协议	Sumcheck协议	Shamir's协议

Quantified Boolean Formulas

完全量化的布尔公式（Fully Quantified Boolean Formulas）的逻辑表达如下： \[ \forall x_1 \exists x_2\exists x_3\,\, (x_1\land x_2)\vee x_3\\ \underbrace{\forall x_1 \exists x_2\forall x_3}_{\text{每一个变量都通过 }\forall,\exists\text{ 量化}} \,\, \underbrace{(x_1\land x_2)\vee x_3}_{布尔公式} \] Note：\(\mathrm{NP}\sim \{\phi|\exists x_1\exists x_2\dots\exists x_n,\phi(x_1,\dots,x_n)=1\}\)​

​ \(\mathrm{coNP}\sim \{\phi|\forall x_1\forall x_2\dots\forall x_n,\,\phi(x_1,\dots,x_n)\not=1\}\)​

\(\mathrm{TQBF}\)即为True Quantified Boolean Formulas，即\(\mathrm{TQBF}=\{\phi(x_1,\dots,x_n) \text{s.t. }\forall x_1\exists x_2\forall x_3\dots,\,\phi(x_1,\dots,x_n)=1\}\)​，\(\mathrm{TQBF}\)是一个\(\mathrm{PSPACE}\)完全问题。

Arithmetization for TQBF

参考之前算术化\(\mathrm{\#SAT}\)问题的方法，我们可以将公式和量词分别进行量化：

• 公式（formula）：我们使用算术化\(\mathrm{\#SAT}\)的方法：\(\phi(x_1,\dots,x_n)\mapsto p(x_1,\dots,x_n) \text{ s.t. } p|{}_{\{0,1\}^n}\equiv \phi \,\&\, \deg_{\text{ind}}\leq|\phi|\)​
• \(\forall\) ：类似于合取，\((\forall x_i,\phi(\dots,x_i,\dots)=\phi(\dots,0,\dots)\land\phi(\dots,1,\dots)\)​
  • 我们定义\(\Pi_{x_i}p(\dots,x_i,\dots)=p(\dots,0,\dots)\cdot p(\dots,1,\dots)\)
• \(\vee\)：类似于析取，\((\exists x_i,\phi(\dots,x_i,\dots)=\phi(\dots,0,\dots)\vee\phi(\dots,1,\dots)\)
  • 我们定义\(\coprod_{x_i}p(\dots,x_i,\dots):=1-(1-p(\dots,0,\dots)\cdot p(\dots,1,\dots))\)

\(p|{}_{\{0,1\}^n}\equiv \phi\)，并且我们得到的多项式可以扩展到任何有限域。

Degree Reduction

现在我们需要一个协议能够验证我们算术化出来的多项式，我们借鉴Sumcheck protocol的方法，每次剥离掉一个变量 \[ p_1(x_1)=\coprod_{x_2}\prod_{x_3}p(x_1,x_2,\dots,x_n) \] 然而，该方法也会引入一个问题，因为存在大量的合取和析取，每次都会导致多项式的次数上升，会导致最后的\(p_1\)的次数达到\(2^{n-1}\)，是一个无法接受的次数，如果我们想发送这个多项式，需要发送\(2^{n-1}+1\)​个系数，对通信带来了巨大的开销，因此我们需要进行Degree Reduction。

每次合取或析取都会使次数翻倍，因此是\(2^{n-1}\)

但是我们可以通过观察发现，只能取布尔值的变量有一个特点\(x^n=x,x\in\{0,1\}\)，因此我们可以直接将所有的次数化为1。我们定义一个新的符号\(\nabla\) \[ \nabla_{x}x^n=x \] 因此原来的算术化多项式可以转化为： \[ \prod_{x_1}\nabla_{x_1}\coprod_{x_2}\nabla_{x_1}\nabla_{x_2}\prod_{x_2}\nabla_{x_1}\nabla_{x_2}\nabla_{x_3}\dots\prod_{x_n}\nabla_{x_1}\nabla_{x_2}\dots\nabla_{x_n}p(x_1,x_2,\dots,x_3) \]

Shamir's Protocol

对于\(\mathrm{TQBF}\)问题，我们需要验证 \[ \prod_{x_1}\nabla_{x_1}\coprod_{x_2}\nabla_{x_1}\nabla_{x_2}\prod_{x_2}\nabla_{x_1}\nabla_{x_2}\nabla_{x_3}\dots\prod_{x_n}\nabla_{x_1}\nabla_{x_2}\dots\nabla_{x_n}p(x_1,x_2,\dots,x_3)=\gamma \] 其中共有运算符\(k=n+\dfrac{(1+n)*n}{2}=\dfrac{(3+n)*n}{2}\)​，我们每次消去一个，可以得到与Sumcheck十分相似的协议 \[ \begin{align*} &\text{for j=1,...,k in round j:}\\ &\quad\text{Prover}\quad\quad\quad\quad\quad\quad\quad\quad\quad \text{Verifier}\\ &\quad\quad\quad\quad\quad O_j\dots O_k\,p\overset{?}{=}\gamma_{j-1}\\ &\quad———\widetilde{p_j}\in\mathbb{F}[x]\longrightarrow i_j\in[n] \text{ is var of }O_j \\ &\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \text{check }\widetilde{p_j}\text{ vs }\gamma_{j-1}\\ &\quad\longleftarrow w_{i_j}\in\mathbb{F}[x]———\quad\quad w_{i_j}\leftarrow\mathbb{F}\quad\quad\\ &\quad\quad\quad\quad\quad\quad\quad\quad\quad\gamma_{j}:=\widetilde{p_j}(w_{i_j})\,\&\,w_{i_j}:=w_i\\ &\text{after k rounds, verifier check } p(w_1,w_2,\dots,w_n)\overset{?}{=}\gamma_k\\ \end{align*} \] 该协议共交互k轮，对于不同的符号有不同的check方式：

• 如果\(O_j=\prod_{x_{i_j}}\)，那么验证\(\widetilde{p_j}(0)\cdot\widetilde{p_j}(1)\overset{?}{=}\gamma_{j-1}\)​
• 如果\(O_j=\coprod_{x_{i_j}}\)，那么验证\(1-(1-\widetilde{p_j}(0))\cdot(1-\widetilde{p_j}(1))\overset{?}{=}\gamma_{j-1}\)
• 如果\(O_j=\nabla_{x_{i_j}}\)，那么验证\(\nabla_{x_i}\widetilde{p_j}(w^{old})\overset{?}{=}\gamma_{j-1}\)

Completeness

对于符号为\(\prod_{x_{i}}\)或\(\coprod_{x_{i}}\)的情况，我们有 \[ \prod_{x_i}O_{j+1}\dots p(w_1,w_2,\dots,w_{i-1},x_i,\dots,x_n)=\gamma_{j-1} \] 诚实Prover发送\(p_j(x_i)=O_{j+1}\dots p(w_1,w_2,\dots,w_{i-1},x_i,\dots,x_n)\)

Verifier验证\(\gamma_{j-1}=p_j(0)\cdot p_j(1)\)，并且进一步输出\(\gamma_j=O_{j+1}\dots p(w_1,w_2,\dots,w_{i-1},w_{i_j},\dots,x_n)\)

进一步进行验证，最终接受概率为\(1\)。

对于符号为\(\nabla_{x_i}\)的情况，我们有 \[ \nabla_{x_i}O_{j+1}\dots p(w_1,\dots,w_{i},\dots,w_s,x_{s+1},\dots,x_n)=\gamma_{j-1} \] 诚实Prover发送\(p_j(x_i)=O_{j+1}\dots p(w_1,\dots,w_{i-1},x_i,\dots,w_s,x_{s+1},\dots,x_n)=\gamma_{j-1}\)

Verifier验证\(\gamma_{j-1}=\nabla_{x_i}p_j(w_i)\)，并且进一步输出\(\gamma_j=O_{j+1}\dots p(w_1,\dots,w_{i},w_{i_j},\dots,w_s,x_{s+1},\dots,x_n)\)

进一步进行验证，最终接受概率为\(1\)。

Soundness

Soundness主要分为两种不同的情况：

• 对于符号为\(\prod_{x_{i}}\)或\(\coprod_{x_{i}}\)的情况，我们有恶意Prover发送\(\widetilde{p_j}(x_i)\)，Verifier验证\(\gamma_{j-1}=p_j(0)\cdot p_j(1)\overset{?}{=}\widetilde{p_j}(0)\cdot\widetilde{p_j}(1)\)，接受概率为\(\dfrac{1}{\mathbb{|F|}}\)

• 对于符号为\(\nabla_{x_i}\)的情况，我们有恶意Prover发送\(\widetilde{p_j}(x_i)\)，Verifier验证\(\gamma_{j-1}=\nabla_{x_i}p_j(w_i)\overset{?}{=}\nabla_{x_i}\widetilde{p_j}(w_i)\)，接受概率为\(\dfrac{2}{\mathbb{|F|}}\)或\(\dfrac{3m}{\mathbb{|F|}}\)。

所以综合的Soundness为\(n\cdot\dfrac{1}{\mathbb{|F|}}+n\cdot\dfrac{3m}{\mathbb{|F|}}+\dfrac{n^2-n}{2}\cdot\dfrac{2}{\mathbb{|F|}}=\dfrac{3mn+n^2}{\mathbb{|F|}}\)​

\(\mathrm{TQBF}\in \mathrm{PSPACE-complete}\)

Todo;

Public Coins

Public Coins vs Private Coins

从前面的课程中我们可以已经知道了随机性对于IP至关重要，分为不同的形式：

1. 在GNI的交互式证明中，Verifier的随机比特b是保密的
2. 在TQBF的交互式证明中，Verifier的随机数w是作为消息直接发送给Prover的

上述两个证明就对应于交互式证明中的两个不同的证明方法：Public Coins和Private Coins

[!NOTE]

后面我还会学到随机性对于实现零知识证明也是至关重要的

之所以叫Public Coins和Private Coins，笔者认为是最开始提出IP的时候，讲随机数是通过不断抛硬币来得到的，是否将随机数公开就是是否将自己抛硬币的结果公开，因此就有了Public Coins和Private Coins

我们给出以下定义：如果一个交互式证明中Verifier的消息都是新鲜从已定长度的均匀随机分布中抽取的，那么这个交互式证明就是Public Coins；否则就是Private Coins

AM[K]/MA[K]就是由Verifier/Prover先发送消息，并且可以通过k轮Public-coin交互式证明来确定是否为True的语言集合

AM和MA来源于Arthur-Merlin，其中Arthur代表Verifier，Merlin代表Prover（wizard，hhh）

引理：\(\forall \mathrm{K},\mathrm{AM[K]/MA[K]}\subseteq \mathrm{IP[K]}\)

证明很简单，因为无论是MA还是AM都只是Public-coin的交互式证明，而IP包含了Public-coin和Private-coin交互式证明

有一个非常有意思的结论：\(\forall\mathrm{K},\mathrm{IP[K]}\subseteq \mathrm{AM[K+1]}\)​​​，但是证明通用的结论是十分困难的，在本篇博客中，我们会引用之前所了解过的GNI问题来讲解

Graph Non-Isomorphism

我们定义图同构（Graph Isomorphism）问题：给定\((G_0,G_1),S:=\{H|H\equiv G_0 \text{ or } H\equiv G_1\}\)

我们可以通过是否与\(G_0\)或\(G_1\)同构证明\(H\in S\)

• \(G_0 \equiv G_1 \longrightarrow |S|=n!\)
• \(G_0 \not\equiv G_1 \longrightarrow |S|=2\cdot n!\)​

接下来我们就可以通过判断\(|S|\)​的大小来判断GNI问题。

Pairwise Independent Hashing

我们首先给出定义：

一个函数族\(H_{m,\ell}=\{h:\{0,1\}^m\rightarrow\{0,1\}^\ell\}\)是成对独立的，如果有\(\forall \text{ distinct } x,x^\prime\in\{0,1\}^m,y,y^\prime\in\{0,1\}^\ell,\Pr_{h\leftarrow H_{m,\ell}}[h(x)=y\land h(x^\prime)=y^\prime]=\dfrac{1}{2^{2\ell}}\)​

Set lower bound protocol

我们令\(S\subseteq\{0,1\}^m\)，并且满足\(S\in\mathrm{NP}\)（我们可以在Prover的帮助下验证\(x\in S\)）

Set lower bound protocol可以帮助我们实现以下功能：

• 如果\(|S|\ge B\)，Verifier接受
• 如果\(|S|\leq \dfrac{B}{2}\)，Verifier拒绝

image-20240213105327162

我们对Set lower bound protocol进行分析：

Soundness：

如果\(|S|\leq \dfrac{B}{2}\)，那么我们有\(\Pr_{h,y}[\exists x\in S:h(x)=y]\leq\sum_{x\in S}\Pr_{h,y}[h(x)=y]=\dfrac{|S|}{2^\ell}\leq\dfrac{1}{2}\cdot\dfrac{B}{2^\ell}\leq\dfrac{1}{4}\)

Completeness：

如果\(|S|\ge B\)，那么我们有

Public Coin Interactive Proof for GNI

我们令\(S:=\{H\in\{0,1\}^{n^2}|H\equiv G_0 \text{ or } H\equiv G_1\}\)​

image-20240213110914995

Perfect Completeness for Public Coins

Todo