Why and How zk-SNARK Works Definitive Explanation

Why and How zk-SNARK Works: Definitive Explanation

Abstract

本篇论文对于zk- SNARK做了一个简单的阐述，不仅解释了它是如何工作的，更解释了它为什么如此工作和它如何变成这样。

1. Introduction

零知识简洁非交互式知识论证（Zero-knowledge succinct non-interactive arguments of knowledge, zk-SNARK）是一种在不揭露任何其他信息的情况下，证明论述为true的一种优雅的方法。

零知识证明有很多的应用场景：

证明关于隐私信息的论述，例如：证明A的银行账户里有比X更多的钱
匿名授权，例如：证明请求者R有权访问网站的限制区域，而不透露其身份（例如登录名、密码）
匿名支付，例如：在不透露收入的情况下纳税
外包计算，例如：外包昂贵的计算，并在不重做执行的情况下验证结果是否正确

尽管表面上听起来很棒，但其背后的方法是数学和密码学的一大奇迹，自1985年在《The Knowledge Complexity of Interactive Proof-systems》[GMR85]中引入以来，人们已经研究了40年，随后引入了在区块链环境中特别重要的非交互证明[BFM88]。

零知识证明具有以下性质：

完备性（Completeness）：如果陈述属实，则证明者可以说服验证者
稳健性（Soundness）：证明者无法说服证明者相信虚假陈述
零知识（Zero-knowledge）：证明只会揭示陈述是否属实，而不是其他

2. The Medium of a Proof

假设我们想证明一个长为10数组中每个元素都为1，我们采用每次检查1个元素之后shuffle的方法：

Completeness：如果数组中的元素均为1，那么我们一定能够说服Verfier
Soundness：如果数组中存在0，我们计最好情况，数组中包含1个0，那么第一次check我们被欺骗的概率为$90\%$，第二次为$90\%^2=81\%$，通过$\lceil\log_{0.9}{0.05} \rceil=29$次重复，我们可以将被欺骗的概率降至$5%$以下

但是上述方法的复杂度较高，其需要check的次数与数组中元素的个数成线性相关。因此我们可以采用多项式的方法，将所需要的约束用多项式表示，根据Schwartz-Zipple-Demillo-Lipton（SZDL）定理，我们只需要验证很大的定义域内的一个input对应的output，就可以以极大的概率确定该多项式的正确性。

Theorem 1 (Schwartz, Zippel). Let \[ P \in R\left[x_1, x_2, \ldots, x_n\right] \] be a non-zero polynomial of total degree $d \geq 0$ over an integral domain $R$. Let $S$ be a finite subset of $R$ and let $r_1, r_2, \ldots, r_n$ be selected at random independently and uniformly from S. Then \[ \operatorname{Pr}\left[P\left(r_1, r_2, \ldots, r_n\right)=0\right] \leq \frac{d}{|S|} . \]

Equivalently, the Lemma states that for any finite subset $S$ of $R$, if $Z(P)$ is the zero set of $P$, then \[ \left|Z(P) \cap S^n\right| \leq d \cdot|S|^{n-1} . \]

Proof. The proof is by mathematical induction on $n$. For $n=1$, as was mentioned before, $P$ can have at most $d$ roots. This gives us the base case. Now, assume that the theorem holds for all polynomials in $n-1$ variables. We can then consider $P$ to be a polynomial in $x_1$ by writing it as \[ P\left(x_1, \ldots, x_n\right)=\sum_{i=0}^d x_1^i P_i\left(x_2, \ldots, x_n\right) . \]

Since $P$ is not identically 0, there are some $i$ such that $P_i$ is not identically 0. Take the largest such $i$. Then $\operatorname{deg} P_i \leq d-i$, since the degree of $x_1^i P_i$ is at most d.

Now we randomly pick $r_2, \ldots, r_n$ from $S$. By the induction hypothesis, $\operatorname{Pr}\left[P_i\left(r_2, \ldots, r_n\right)=0\right] \leq \frac{d-i}{|S|}$. If $P_i\left(r_2, \ldots, r_n\right) \neq 0$, then $P\left(x_1, r_2, \ldots, r_n\right)$ is of degree $i$ (and thus not identically zero) so \[ \operatorname{Pr}\left[P\left(r_1, r_2, \ldots, r_n\right)=0 \mid P_i\left(r_2, \ldots, r_n\right) \neq 0\right] \leq \frac{i}{|S|} . \]

If we denote the event $P\left(r_1, r_2, \ldots, r_n\right)=0$ by $A$, the event $P_i\left(r_2, \ldots, r_n\right)=0$ by $B$, and the complement of $B$ by $B^c$, we have \[ \begin{aligned} \operatorname{Pr}[A] & =\operatorname{Pr}[A \cap B]+\operatorname{Pr}\left[A \cap B^c\right] \\ & =\operatorname{Pr}[B] \operatorname{Pr}[A \mid B]+\operatorname{Pr}\left[B^c\right] \operatorname{Pr}\left[A \mid B^c\right] \\ & \leq \operatorname{Pr}[B]+\operatorname{Pr}\left[A \mid B^c\right] \\ & \leq \frac{d-i}{|S|}+\frac{i}{|S|}=\frac{d}{|S|} \end{aligned} \]

具体流程如下：

Verifier选择一个随机数$x$并且在本地运算多项式
Verifier将$x$发送给Prover，并且要求它运算质询中的多项式
Prover计算多项式在$x$处的取值，并且将结果发送给Verifier
Verifier验证结果的正确性，并且给出accept/reject

3. Non-Interactive Zero-Knowledge of a Polynomial

3.1 Proving Knowledge of a Polynomial

多项式的表示方法

系数表达
- 求值：霍纳法则 $O(n)$复杂度
- 加法：$O(n)$复杂度
- 乘法：$O(n^2)$复杂度（因为向量$a$中的每个系数必须与向量$b$中的每个系数相乘，我们目前的问题就在于优化乘法）
点值表达
- 插值：拉格朗日插值 $O(n^2)$复杂度
- 加法：$O(n)$复杂度
- 乘法：$O(n)$复杂度

多项式的快速乘法

通过前面的介绍，我们有了两种计算多项式乘法的方法：

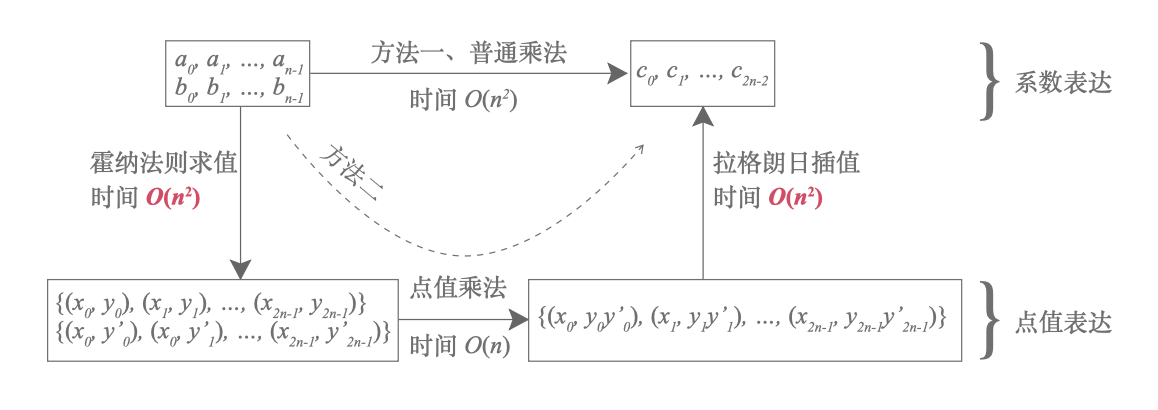
图中的两种方法的时间复杂度都是 $ (n^2)$。在方法二中, 我们可以采用任何点作为求值点, 但通过精心地挑选求值点, 可以把多项式“系数表达”和“点值表达”之间转化所需的时间复杂度变为 $\Theta(n \lg n)$。

离散傅里叶变换 (DFT)

在进一步介绍前, 我们先了解一下离散傅里叶变换 (DFT)。向量 $a=\left(a_0, a_1, \cdots, a_{n-1}\right)$ 的离散傅里叶变换为另外一个向量 $y=\left(y_0, y_1, \cdots, y_{n-1}\right)$, 该向量中每个元素的定义为: \[ y_k=\sum_{j=0}^{n-1} a_j w_n^{k j} \]

上式中 $w_n^k, k=0,1, \cdots, n-1$ 分别是满足 $w^n=1$ 的 $n$ 个单位复数根中的第 $k$ 个。

如果我们恰好在 “单位复数根” $w_n^k$ 处求值 $A(x)$, 则显然这样得到的 $A\left(w_n^k\right)=\sum_{j=0}^{n-1} a_j w_n^{k j}$ 就是系数向量 $a=\left(a_0, a_1, \cdots, a_{n-1}\right)$ 的离散傅里叶变换。

快速傅里叶变换 (FFT) 是计算离散傅里叶变换（DFT）的快速算法, 它的时间复杂度是 $\Theta(n \lg n)$; 同样快速傅里叶逆变换（IFFT）是计算离散傅里叶逆变换（IDFT）的快速算法, 它的时间复杂度也是 $\Theta(n \lg n)$ 。

FFT加快多项式乘法

基于前面的介绍, 我们可以得到了下图的方法来加快多项式乘法的计算, 它的时间复杂度为 $(n n) $

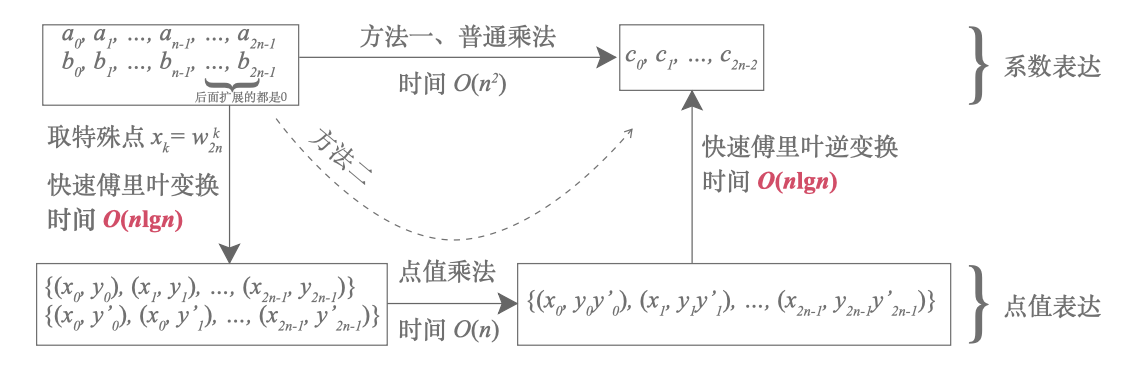
下面是使用 FFT 加快加速多项式乘法计算的具体操作步骤: 1. 加倍次数界: 通过加入 $n$ 个系数为 0 的高阶系数, 把多项式 $A(x)$ 和 $B(x)$ 变为次数界为 $2 n$ 的多项式, 并构造其系数表达; 2. 求值: 通过应用 $2 n$ 阶的 FFT 计算出 $A(x)$ 和 $B(x)$ 的长度为 $2 n$ 的点值表达。这些点值表达中包含了两个多项式在 $2 n$ 次单位根处的取值; 3. 逐点相乘: 把 $A(x)$ 的值与 $B(x)$ 的值逐点相乘, 可以计算出多项式 $C(x)=A(x) B(x)$ 的点值表达, 这个表示中包含了 $C(x)$ 在每个 $2 n$ 次单位根处的值; 4. 插值: 通过对 $2 n$ 个点值对应用 IFFT, 计算其逆 DFT, 就可以构造出多项式 $C(x)$ 的系数表达。

3.2 Factorization

代数基本定理指出，任何可解多项式都可以分解成线性多项式(即一次多项式)，即都可以表示成如下形式： \[ (x-a_0)(x-a_1)\dots(x-a_n)=0 \] 如果这些因子中的任何一个是零，那么整个方程就是零，因此所有的$a_s$即为方程所有解。

如果一个Prover想证明一个多项式有已知的几个根（witness），则可知原多项式为该“归零多项式”的倍数，即有： \[ p(x)=h(x)\cdot t(x) \] 归零多项式$t(x)$也被称为目标多项式（target polynomial）。

我们可以通过以下流程来检查多项式的性质：

Verifier随机选取一个随机值$r$，计算$t=t(r)$并且将$r$发送给Prover
Prover计算$h(x)=\frac{p(x)}{t(x)},p(r),h(r)$，并且将所得的$p,h$发送给Verifier
Verifier验证$p=h\cdot t$，如果等式成立，则有$p(x)$为$t(x)$的倍数

如果$p(x)$不是$t(x)$的倍数，则有 \[ h(x)=\dfrac{p(x)}{t(x)}=\hat{h}(x)+\dfrac{r(x)}{t(x)} \] 由于 $r(x) / t(x)$ 非零，当$x$随机取值时，最后的余项大概率不是整数 (但仍有非 negligible 的概率是整数)，故无法通过验证。

但是该方案仍存在一些问题：

在$x$随机取值的情况下，仍有non-negligible的概率$r(x)/t(x)$为整数，导致不合法证明的产生。
由于目前运算并非在有限域下，上述协议只能应用于多项式系数为整数的情况，对于分数系数的多项式无法进行验证。
Prover 可能根本不知道一个合法的 $p(x)$, 他可以直接计算出 $t(s)$ 的值（因为多项式 $t(x)$ 所有人都知道, $s$ 已由 Verifier 给出), 然后随机取一个数字 $h$, 或者随机构造一个多项式 $h(x)$, 然后将 $h=h(s)$ 和 $p=h \cdot t(s)$ 发给 Verifier, 仍会通过验证。
Prover知道随机点$x=r$，所以他可以构造在$r$处与$t(r)·h(r)$有一个公共点的任何多项式。
后续我们仍需要对 Prover 给出的 $p(x)$ 添加某些限定，如规定其次数不超过 $d$，或者不含某些项(如不含常数项，$x^2$ 项等)，上述协议无法扩展出这些限定要求。

3.3 Homomorphic Encryption

离散对数问题：给定$y=g^x$，通过$y$计算出$x$的值是十分困难的

CDH假设：给定$g^a,g^b$，算出$g^{ab}$的值是困难的

由此我们可以得到一个同态加密的函数（个人认为只是一种Homomorphic commitment）： \[ E(x)=g^x \] 满足加法同态：$E(x_1)*E(x_2)=g^{x_1}\cdot g^{x_2}=g^{x_1+x_2}$，但不满足乘法同态

现在我们可以将上述方案修改如下：

Verifier随机选取一个随机值$r$，计算$E(s^0),E(s^1),E(s^2)\dots E(s^d)$并发送给Prover
Prover 通过收到的加密数据计算 $E(h(s))$ 和 $E(p(s))$，具体方法为计算 $E\left(s^0\right)^{c_0}\cdot E\left(s^1\right)^{c_1} \ldots E\left(s^d\right)^{c_d}$，其中 $c_0, \ldots, c_d$ 为对应的多项式系数 $(h(x)$ 或 $p(x))$，并发送给 Verifier
Verifier 计算$t(s)$并验证$E_p=E_h^{t(s)}$

由于$E(x)$只满足加法同态，不满足乘法同态，因此可以保证安全性。

我们接下来分析上述协议如何帮助我们解决上一章的几个问题：

对于问题 1，如果 $t(x)$ 不能整除 $h(x)$，如上一章节所述，存在非零余项 $r(s)$，且 Prover 需要提供$E(\hat{h}(s)+r(s) / t(s))=E(\hat{h}(s)) \cdot E(r(s) / t(s))$ 。其中 $E(\hat{h}(s)), E(r(s)), E(t(s))$均可以算出，但是 $E(r(s) / t(s))$ 却因为加密函数 $E(x)$ 不满足乘除同态性而无法计算，且我们也不知道$s$的具体取值，因此无法直接得到$r(s)/t(s)$，从而直接计算$E(r(s)/t(s))$（即使 $r(s) / t(s)$ 是整数, 在模 $p$ 意义下整数和分数已没有区别）这意味着 ${t}(x)$ 必须完全整除（不能只对某些 $s$ 取值整除） $h(x)$ 证明才能合法。
对于问题2，由于在模 $p$ 意义下分数已经化成了整数，对于分数多项式也需要完全整除才能生成合法的证明。(一般而言，所有实数域上的运算法则在模 $p$ 意义下也成立)
对于问题3，首先，由于不知道 $s$ 的值，Prover 不能直接算出 $t(s)$ 再随便乘个数发给 Verifier，但他仍然可以算出 $E(t(s))$ 的值然后再进行 $h$ 次方得到 $E(p(s))$ 发给 Verifier 通过验证。（但是我认为这个问题不在本协议的考虑范围之内，因为本协议要verify的是Prover是否知道一个满足该性质的多项式，有了$t(x)$Prover一定能知道一个满足该性质的多项式，这么看来这个协议好像也没有什么实用价值，仅供学习使用？）
对于问题4，目前仅能对多项式的最高次数做限定。

虽然在这种协议中证明者的灵活性是有限的，但他仍然可以使用任何其他手段来伪造证明，例如，如果证明者声称仅使用$s^3$和$s^1$就有满足的多项式，这在当前的协议中是不可能验证的。

3.4 Knowledge of Polynomial

关于一个多项式的知识就是其系数$c_0,c_1,c_2\dots c_d$的知识，我们在协议中使用这些系数的方式是通过对相应的加密值的幂进行指数运算$E(s^i)^{c_i}=g^{c_i \cdot s^i }$，我们可以通过KEA假设来保证Prover对于多项式的知识：

KEA, Knowledge-of-Exponent Assumption：给定一组 $a, a^{\prime}$ 满足 $a^{\prime}=a^\alpha$ (这个 $a^{\prime}$ 称作偏移量), 在不知道 $\alpha$ 的情况下, 如果有人能够给出另外一组数 $\left(b, b^{\prime}\right)$ 使得 $b^{\prime}=b^\alpha$, 那么一定有 $b=a^c$ 。

因为Prover无法获取$\alpha$的值，因此它一定知道$c$的值。

这一小节原论文中讲是为了避免上述问题3随机常数项的使用，但是以笔者目前的认知，感觉好像抵抗不了。（由于笔者目前所学浅陋，可能会有错误理解，渴望教教🥺）

即使是有KEA约束，在提供有$E(s^0)$和$E(\alpha s^0)$的情况下，我还是可以继续构造上述的攻击：$z_h=E(s^0)^r=g^r, z_h^\prime = E(\alpha s^0)^r=g^{\alpha r}$，因为t(x)是公开的,因此我们可以非常轻松的得到t(s),从而$z_p=z_h^{t(s)},z_p^\prime=z_h^{\prime{t(s)}}$貌似还是可以正常攻击。

对于文中所说的