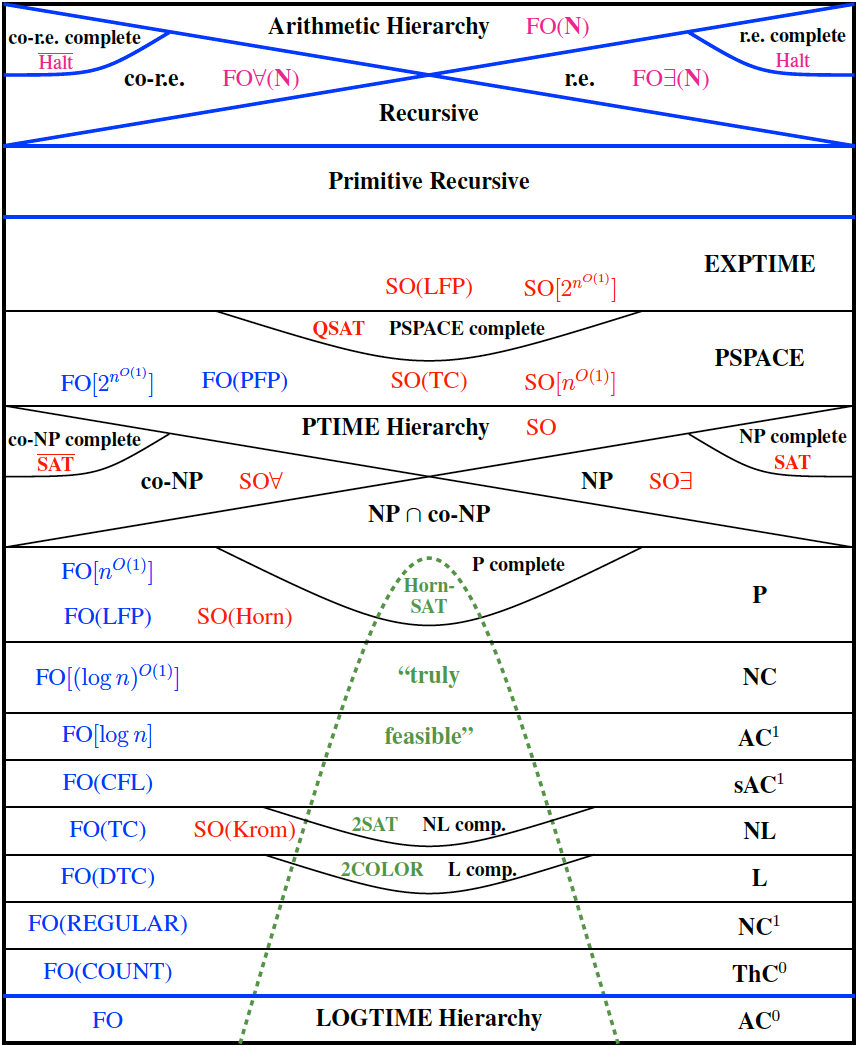
Complexity Class

在计算复杂度理论中，一个复杂度类指的是一群复杂度类似的问题的集合。一个典型的复杂度类的定义有以下形式：

• 可以被同一个抽象机器M使用O(f(n))的资源R所解决的问题的集合（n是输入资料的大小）。

L （Logarithm space class)

L，也称为LSPACE或DLOGSPACE，是能被确定型图灵机利用对数空间解决的判定问题集合。

对数空间是指与输入规模成对数大小关系的可写的储存空间，大多数对数空间（LOGSPACE）算法以这种方式储存。

重要的相关未解问题包括复杂度类L和P是否恒等（L = P）及复杂度类L和NL是否恒等（L = NL）。 目前已知有以下重要性质：

• \(\mathrm{L} \subseteq \mathrm{NL} \subseteq \mathrm{P}\)
• \(\mathrm{NC}^1 \subseteq \mathrm{L} \subseteq \mathrm{NL} \subseteq \mathrm{NC}^{2}\)

P（Polynomial time class）

P，也称为PTIME、DTIME(\(n^{O(1)}\)​)，是可用确定型图灵机以多项式时间解决的判定问题集合。

形式化定义：如果一个语言L属于复杂度类P，当且仅当存在一个确定型图灵机满足以下条件：

• \(M\)在所有输入上以多项式时间运行
• 对于所有属于\(L\)的\(x\)，\(M\)输出为1
• 对于所有不属于\(L\)的\(x\)，\(M\)​​​输出为1

\(\mathrm{P}\)也可以被视为一种布尔电路的uniform family。语言\(L\)在\(\mathrm{P}\)中，当且仅当存在布尔电路\(\left\{C_n: n \in \mathbb{N}\right\}\)的多项式时间uniform family满足

• 对于所有\(n \in \mathbb{N}，C_n\)接受\(n\)位作为输入，并且输出为1比特

• 对于所有属于\(L\)的\(x\)，\(C_{|x|}(x)=1\)

• 对于所有不属于\(L\)的\(x\)，，\(C_{|x|}(x)=0\)

电路定义可以削弱为仅使用对数空间uniform family，而无需更改复杂度类。

uniform family在Alessandro的CS294里面IP#6里面有提到过这个概念，个人理解uniform大概想表达的意思应该是均匀，完整的整个电路因为这些均匀重复的信息可以用很少的描述（description）去表达出来。

这种uniform电路有一个性质就是可以用少于整个电路大小（|C|-size）的描述去完整的表达这个电路，也就意味着可能不需要完全read这个电路就能求出结果。

在此处仅使用对数空间uniform family，是因为\(2^{O(\log n)}=n^{O(1)}\)，仅使用对数空间就能表现出来所有的组合。

P通常表示那类可以“可被高效解决”或“易于处理（tractable）”的可计算型问题，就算指数级非常高也可以算作“易于处理”，例如RP与BPP问题。当然P类别存在很多现实处理上一点也不易于处理的问题，例如一些至少需要\(n^{1000000}\)​指令来解决的问题，但是他也是多项式时间，并非指数时间。

P包含了很多已知的自然问题，例如决定性版本的线性规划，计算最大公因数，以及发现最大匹配。在2002年，判别一个数是否为质数也被人解出是一个P问题。

一个判定算法使用了\(O(\log n)\)的空间就不可能使用超过\(2^{O(\log n)}=n^{O(1)}\)的时间，因为这是所有可能组合方式的总数，因此L是P的子集合。另一个重要问题是：L是否相等于P？我们已知P=AL（问题可在对数存储器上以交替式图灵机解决的问题之集合），而P也已知不大于PSPACE（可在多项式空间判定的问题）。再一次，我们面对P是否等于PSPACE的未知问题。整理一下上述问题： \[ \mathrm{L} \subseteq \mathrm{AL}=\mathrm{P} \subseteq \mathrm{NP} \subseteq \mathrm{PSPACE} \subseteq \mathrm{EXPTIME} \]

NP （Non-deterministic Polynomial time class）

NP有两种定义方式：

• 非确定型图灵机可以在多项式时间内解决（solvable）的判定问题集合。
• 确定型图灵机可以在多项式时间内验证（decidable）的判定问题集合。

形式化定义：

复杂性类NP可以用NTIME定义如下： \[ \mathrm{NP}=\bigcup_{k \in \mathbb{N}} \operatorname{NTIME}\left(n^k\right) \] 其中\(\operatorname{NTIME}\left(n^k\right)\)是非确定性图灵机可以在\(O\left(n^k\right)\)时间内解决的决策问题集。

也可以使用确定性图灵机作为验证器来定义NP。语言\(L\)在NP中，当且仅当存在多项式\(p\)和\(q\)，以及确定性图灵机\(M\)，使得

• 对于所有\(x\)和\(y\)，机器\(M\)在输入\((x, y)\)上以时间\(p(|x|)\)运行。

• 对于\(L\)中的所有\(x\)，存在一个长度为\(q(|x|)\)的字符串\(y\)，使得\(M(x, y)=1\)。

• 对于所有不在\(L\)中的\(x\)和长度为\(q(|x|)\)的所有字符串\(y\)，\(M(x,y)=0\)。

其中的\(x\)和\(y\)，我们可以理解为零知识证明中的statement和witness（assignment）。

很容易看出，复杂度类P都包含在NP中，因为如果一个问题可以在多项式时间内解决，那么也可以通过找出解决方案解决问题来实现在多项式时间内验证。

但NP包含更多问题，其中最难的问题被称为NP完全（NP-complete）问题，NP中的任何问题都可以归约为NP完全问题\(\mathrm{NP}\propto \mathrm{NP-complete}\)，因此在多项式时间内解决此类问题的算法也能够在多项式时间内解决任何其他NP问题。

最重要的P与NP（“P = NP？”）问题，询问是否存在解决NP完全的多项式时间算法，并通过推论解决所有NP问题。

NP包含在PSPACE中，因为多项式时间机器只能读取多项式长度的字符串，所以我们可以使用PSPACE机器遍历所有的证明字符串，并将每个字符串反馈给多项式时间验证器。

SAT（Satisfiability）问题是令$ x_1，x_2,,x_n\(代表布尔变量(boolean variables)。令\)-x_i$ 代表 $ x_i$​ 的相反数（negation）。一个布尔公式是将一些布尔变量及其相反数利用而且（and）和或（or）所组成的表达式。满足问题是判断是否存在一种指定每个布尔变量真假值的方式，使得一个布尔公式为真。2SAT问题是NL-complete问题，3SAT是NP-complete问题

我们利用SAT问题给出NP-complete问题的另一种定义：

• 一个问题 L 被称为是 NP-hard，当且仅当，SAT问题可以归约为 L。 SAT问题是 NP 中的难题，而 NP-hard 的问题则是SAT问题派生出来的。

• 一个问题 L 被称为是 NP-complete，当且仅当，\(\mathrm{L}\in \mathrm{NP}\) 而且 \(\mathrm{L}\in \mathrm{NP-hard}\) 。

史蒂芬库克(Stephen Cook)证明了一个十分重要的性质:

• 性质(A)：“任一个 NP 内的问题都可以， 在多项式时间内， 被转换成满足问题。
• 性质(B)：“任一个 NP 内的问题都可以， 在多项式时间内， 被转换成任一个 NP-complete 问题。”
• 性质(C): “任一个 NP 内的问题都可以， 在多项式时间内， 被转换成任一个 NP-hard 问题。”
• 性质(D): “满足问题在集合 \(P\) 中， 当且仅当， \(P=N P\) 。”

接下来我们证明3SAT是NP-complete问题：

证明分为两个部分，我们首先需要证明3SAT为NP问题，之后我们证明它是NP-hard问题

3-SAT (3-CNF-SAT) 的描述为：判断是否存在一个布尔表达式 \(C=C_1 \cap C_2 \cap \cdots \cap C_n\)， 其中 \(C_i=x_a \cup x_b \cup x_c\)， 使得 \(C=1\) 。即判断是否存在布尔表达式 \(C=\left(x_a^1 \cup x_b^1 \cup x_c^1\right)\) \(\cap\left(x_a^2 \cup x_b^2 \cup x_c^2\right) \cap \cdots \cap\left(x_a^n \cup x_b^n \cup x_c^n\right)\)​ 为真。

3SAT为NP问题：因此只要给定一个赋值，我们将其带入到布尔表达式，就可以得到验证解的正确性。

3SAT为NP-hard问题：对于每一个SAT 问题， 例如： \[ \left\{\begin{array}{l} C=C_1 \cap C_2 \cap \cdots \cap C_n \\ C_i=x_1^i \cup x_2^i \cup \cdots \cup x_m^i \end{array}\right. \]

他的每一个 \(C_i\) 都是由一定数量的变量组成的。我们分情况对每一组变量做一下操作。

• 若 \(\left|C_i\right|=1\)， 即只有一个变量参与该 \(C_i\) 的组成， 例如 \(C_i=x_1^i\) 。我们将其变换为 \(C_i=x_1^i \cup x_1^i \cup x_1^i\) 。
• 若 \(\left|C_i\right|=2\)， 例如 \(C_i=x_1^i \cup x_2^i\) 。我们将其变换为 \(C_i=x_1^i \cup x_1^i \cup x_2^i\) 。
• 若 \(\left|C_i\right|=3\)， 我们保持其不变。
• 若 \(\left|C_i\right|\ge 4\)， 假设为k，则我们引入k-3个变量，使得 \(C_i=(x_1^i \cup x_2^i \cup y_1^i)\cap(\overline{y_1^i}\cup x_3^i\cup y_2^i)\cap(\overline{y_2^i}\cup x_4^i\cup y_3^i)\cap\dots\cap(\overline{y_{k-3}^i}\cup x_{k-1}^i\cup x_k^i)\)

对于每个SAT的实例， 如果存在一个真值赋值， 则每个子句 \(C_i\) 一定有一个literal为 1 ， 即 \(x_1^i \cup x_2^i \cup \cdots \cup x_m^i\) 中一定有一个为 1 ，

• \(\left|C_i\right|=1\)， 则 \(x_1^i=1\)， \(C_i=1\) 。

• \(\left|C_i\right|=2\)， 则 \(x_1^i \cup x_2^i=1\)， \(C_i=1\) 。

• \(\left|C_i\right|=3\)， 则 \(C_i=1\) 。

• \(\left|C_i\right| \geq 4\)， 则假设:

  • \(x_1^i \cup x_2^i =1\)， 则 \(y_j^i=0(j=1,2,3, \ldots, k-3)\)， 因此 \(C_i=1\) 。

  • \(x_{ k-1}^i \cup x_{k}^i=1\)， 则 \(y_j^i=1(j=1,2,3, \ldots ., k-3)\)， 因此 \(C_i=1\) 。

  • \(x_{j}^i=1(2<j<k-1)\)， 则 \(\overline{y_{a}^i}=0(\mathrm{a} \leq \mathrm{j}-2), y_{ a}^i=0(\mathrm{a} \geq \mathrm{j}-1)\)， 因此 \(C_i=1\) 。

因此得到 \(C\) 的真值赋值 \(t^{\prime}\) 。

故 3-SAT 是 NP 完全的。

co-NP （complement-Non-deterministic polynomial time class）

co-NP是确定型图灵机可以在多项式时间内验证（decidable）反例（no-instance）的判定问题集合，例如素性检测。

形式化定义：co-NP可以通过NP来进行定义 \[ \mathbf{C o N P}:=\left\{L \mid L^{\mathrm{C}} \in \mathbf{N P}\right\} \text { 。 } \] 简单来说，co-NP就是可以高效核实地证明命题为错的问题集合

当一个NP问题询问一个给定的实例是否是YES-实例时，它的补集询问一个实例是否是反例，这意味着补集是co-NP的。原始NP问题的任何是实例都变成了它的补语的反例，反之亦然。

UNSAT是co-NP-complete问题，可以用sumcheck协议通过IP验证，通过将UNSAT问题算术化，之后验证\(\sum{p(x_1,x_2,\dots,x_i)}=0\)。

确定命题逻辑中的范式是否是重言式是co-NP-complete的。

P被认为是严格属于co-NP和NP的，因为P可以在多项式时间内被解决，就可以很容易在多项式时间内判断正例和反例。

整数分解问题：给两个正整数m与n，决定m是否有小于n且大于1的因数。不属于P，但属于\(\mathrm{NP\cup co-NP}\)：

• NP：如果m的确存在一个满足条件的因子，我们可以通过除法来轻易判断
• co-NP：我们可以列举出所有大于或等于n的因子，验证者可以通过乘法和素性测试来确认其有效。

BPP （Bounded-error Probabilistic Polynomial time）

BPP是在多项式时间内以几率图灵机解出的问题集合， 并且对所有的输入，输出结果有错误的概率在1/3之内。BPP这个简写代表"Bounded-error"(有限错误)，"Probabilistic"(几率的)，"Polynomial time"(多项式时间)。

几率图灵机是一个非确定型图灵机，在每个转折点根据某种概率分布随机选择某种可行的转变(transition)。

要是一个问题属于BPP，则存在一个算法，此算法允许转硬币作随机的决定，并在多项式时间内结束。 对这个算法的任何输入，他都要在小于1/3的错误概率之下给出正确判断，不论这一个问题的答案是"正确"或者"错误"。

形式化定义：一个语言 \(L\) 在BPP里面， 当且仅当这语言存在一个概率图灵机 \(M\)， 另

• \(M\) 对任何输入均在多项式时间后停止
• 对任何字串 \(x\) 在 \(L\) 之内， 对 \(M\) 输入 \(x\) 之后， \(M\) 输出 1 的几率大于或者等于 \(2 / 3\)
• 对任何字串 \(x\) 不在 \(L\) 之内， 对 \(M\) 输入 \(x\) 之后， \(M\) 输出 1 的几率小于或者等于 \(1 / 3\)

另外，BPP可以仅以确定性图灵机定义。一个语言 \(L\) 是在BPP里面当且仅当存在一个多项式 \(p\) 和一个决定性图灵机M，满足

• \(M\) 对任何输入均操作多项式时间之内
• 对任何字串 \(x\) 在 \(L\) 之内， 对长度为 \(p(|x|)\) 的任意字串 \(y\)， 满足 \(M(x, y)=1\) 这条件的几率超过或等于 \(2 / 3\)
• 对任何字串 \(x\) 不在 \(L\) 之内， 对长度为 \(p(|x|)\) 的任意字串 \(y\)， 满足 \(M(x, y)=1\) 这条件的几率小于或等于 \(1 / 3\)​

在实际情况下，\(1 / 3\)可以是\(0～1/2\)的任意值，甚至不必是恒定的，例如\(1/2 − n^{−c}\)。可以这么做是因为我们可以通过多次运行并取大多数结果来实现一个更准确的算法。

BPP是大小最大的几个易于处理的问题类别之一，大多数的BPP问题都有高效的概率算法

Diagram of randomised complexity classes

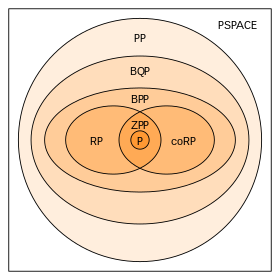
PP （Probabilistic Polynomial time）

PP是概率图灵机在多项式时间内可解的一类决策问题，所有情况下的错误概率都小于1/2。

BPP是PP的一个子集；它可以被视为具有有效概率算法的子集。区别在于允许的错误概率：在BPP中，算法必须给出正确答案（是或否），\(\epsilon > 1/2\)。我们可以多次运行算法，并使用Chernoff边界进行多数投票，以实现任何所需的正确概率。如果\(\epsilon\)接近1/2，这个重复次数会增加，但它不取决于输入大小n。

PH （Polynomial Hierarchy）

PH代表所有在多项式谱系里面的复杂度类并集，亦即： \[ \mathrm{PH}=\bigcup_{k \in \mathbb{N}} \Delta_k \mathrm{P} \] PH最早是由Larry Stockmeyer定义， 是一个受限交替式图灵机(bounded alternating Turing machine)其谱系(hierarchy)的特例。这个复杂度包含于\(\mathrm{P^{PP}}\) (包含问题可以由多项式时间图灵机， 并且能取用PP 神谕的机器所解决的复杂度类。)， \(\mathrm{p^{\# {P}}}\)​ (根据Toda's theorem)， 以及PSPACE里面。

PH有一个简单的逻辑描述方法: PH是一个能以二阶逻辑所表示语言的集合。

PH包含了几乎所有在PSPACE里面有名的复杂度类;举例来说， 像是 P， NP， 和co-NP。甚至还包含了一些概率复杂度类像是BPP和RP。然而，有一些证据指出 BQP(以量子电脑可以在多项式时间之内解决的问题)并不包含在PH里面。

一阶逻辑：只包括取值为论域的个体元素的变量和量词，例如在一阶句子 \(\forall x(x \neq x+1)\) 中变量 \(x\) 被用来表示一个任意的个体。

二阶逻辑：二阶逻辑是一阶逻辑的扩展，通过增加取值在个体的集合上变量和量词。例如，二阶句子 \(\forall S \forall x(x \in S \vee x \notin S)\) 声称对于所有个体的集合 \(S\) 和所有的个体 \(x\)， 要么 \(x\) 在 \(S\) 中要么不在

PSPACE （Polynomial SPACE）

PSPACE是计算复杂度理论中能被确定型图灵机利用多项式空间解决的判定问题集合。

形式化定义：如果规定 \(\operatorname{SPACE}(t(n))\) 为至多 \(t(n)\) 空间内能被确定型图灵机解决的问题的集合 \((t\) 是输入大小 \(n\) 的函数) , 那么, PSPACE可被形式化地定义为: \[ \operatorname{PSPACE}=\bigcup_{k \in \mathbb{N}} \operatorname{SPACE}\left(n^k\right) \]

已经证明PSPACE和NL、P、NP、PH、EXPTIME和EXPSPACE的关系 （注意, \(\subsetneq\) 不是 \(\nsubseteq\) ) : \[ \begin{aligned} & \mathrm{NL} \subseteq \mathrm{P} \subseteq \mathrm{NP} \subseteq \mathrm{PH} \subseteq \mathrm{PSPACE} \\ & \mathrm{PSPACE} \subseteq \mathrm{EXPTIME} \subseteq \mathrm{EXPSPACE} \\ & \mathrm{NL} \subsetneq \mathrm{PSPACE} \subsetneq \mathrm{EXPSPACE} \end{aligned} \]

目前已经知道, 第一行和第二行中至少有一个包含关系为真包含, 但是目前尚未证明任何一个。一般假定所有的包含关系均为真包含。

Complexity Zoo

img